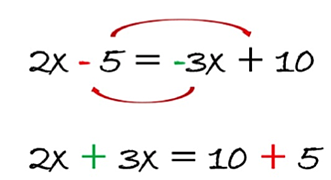Una característica importante de las ecuaciones de primer grado es que en sus componentes no vamos a encontrar exponentes elevados. Aquí vamos a explicar un poco sobre qué es una ecuación y resolveremos ejercicios con ecuaciones de primer grado.
Una ecuación de primer grado es básicamente una igualdad donde están implicados monomios sencillos y monomios con valores no expresados. La idea de resolver una ecuación de primer grado es conocer ese valor que debe tomar la incógnita (muchas veces expresada con la letra X) para que se cumpla la igualdad.
Contenido
Ecuaciones de primer grado y su resolución
Para entender mejor sobre la igualdad tomemos el siguiente ejemplo: 5 + 5 = 10. Del lado izquierdo y derecho cumplen la igualdad. Pero modifiquemos un poco esta expresión: 2 + 8 = 10. Sigue siendo válida. Ahora, escondamos un valor para hacerla una ecuación: x + 8 = 10. Ya tenemos una ecuación de primer grado donde se nos pide encontrar el valor de X, en este ejemplo sencillo sabemos que es 2 pero vamos a ver porque.
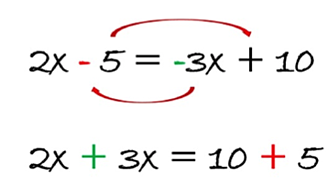
Ejercicio #1
x + 8 = 10
Lo que queremos lograr es conocer el valor de X sin alterar la igualdad. En este caso sencillo despejaremos a X. Como el + 8 es positivo lo vamos a pasar del lado derecho como negativo:
x = 10 – 8
x = 2
Para comprobarlo, sustituimos el resultado en la ecuación original. (2) + 8 = 10 => 10 = 10. Perfecto, se cumple la igualdad.
¿Qué es esto de despejar la incógnita? Lo que hicimos en realidad es lo siguiente:
A la ecuación: x + 8 = 10, le restamos un 8 en ambos lados, tanto derecha como izquierda, para así no alterar la igualdad y poder simplificar y dejar a la X sola o despejada.
x + 8 (- 8) = 10 (-8 ) si te das cuenta, jamas se altero la igualdad ya que en ambos lados se hizo lo mismo (restarle un 8).
x + 0 = 10 – 8
x = 10 – 8
x = 2
Ejercicio #2
2X = 10
Nuevamente, debemos despejar X o dejar sola a X. En este caso, nos conviene dividir ambos lados entre 2 para no alterar la igualdad y poder despejar a X.
2X / 2 = 10 / 2
X = 5
Otra forma de explicar todo lo anterior es: Todo lo que esta sumando de un lado, pasa restando al otro y todo lo que esta multiplicando pasa dividiendo al otro lado. Es chiste es, pasar un valor al otro lado siempre usando su operación inversa. Pero esto se va a explicar usando los siguientes ejemplos.
Ejercicio #3
2X + 1 = 10 – X
Vamos poner de un lado los términos que tienen incógnita y del otro lado los que no tienen incógnita. En este caso, del lado izquierdo pondremos las incógnitas y del derecho los términos simples.
1 … Del lado derecho tenemos – X, esta restando entonces lo pasamos sumando al lado izquierdo:
2X + 1 + X = 10
2 … Del lado izquierdo tenemos a +1, esta sumando entonces lo pasamos restando al lado derecho:
2X + X = 10 – 1
3 … Realizamos las operaciones en ambos lados:
3X = 9
4 … Para despejar 3X, tenemos que pasar ese 3 dividiendo ya que esta multiplicando:
X = 9/3
X = 3
Ejercicio #4
2 (2X + 3) = 12
Para eliminar el paréntesis, tenemos que usar la propiedad distributiva, es decir 2 multiplicarlo por 2X y 6.
1 … Realizamos la propiedad distributiva: 2 * 2X + 2 * 3 = 12
2 … Realizamos la multiplicación: 4X + 6 = 12
3 … Pasamos el término +6 del lado izquierdo al derecho pero restando: 4X = 12 – 6
4 … Realizamos la resta del lado derecho: 4X = 6
5 … Pasamos el 4 multiplicando del lado izquierdo al lado derecho pero dividiendo: X = 6/4
Comprobación:
2 (2[6/4] + 3) = 12
2 ([12/4] + 3) = 12
2 ([3] + 3) = 12
2 (6) = 12
12 = 12
Ejercicio #5
4 + (X/2) = 6
1 … Pasamos el 4 para el lado derecho pero restando: X/2 = 6-4
1.1… Es lo mismo que si restamos un 4 en ambos lados: 4 – 4 + (X/2) = 6 – 4.
2 … Realizamos la resta del lado derecho: X/2 = 2
3 … Pasamos el 2 que esta dividiendo del lado izquierdo al lado derecho pero multiplicando: X = 2 * 2
4 … Tenemos la respuesta: X = 4
Comprobando:
4 + (4/2) = 6
4 + (2) = 6
6 = 6
¿Cómo resolver las ecuaciones de primer grado?
Recuerda que la clave para resolver ecuaciones de primer grado está en respetar la igualdad en ambos lados, puedes realizar las operaciones que quieras en ambos lados a fin de buscar despejar o dejar libre la incógnita. Recuerda el tip: Pasa de un lado a otro siempre con la operación contraria. O si te quieres ver más profesional resolviendo estas ecuaciones, puedes realizar operaciones en ambos lados de la igualdad.
Te recomendamos leer: Los tipos de lenguajes de programación