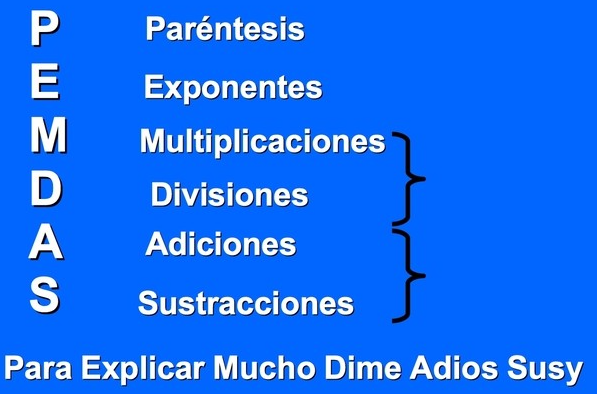
La jerarquía de operaciones es el orden en el que debemos realizar las operaciones. En álgebra es importante respetar esta jerarquía porque de no hacerlo tendremos un resultado erróneo.
Al resolver un ejercicio compuesto de operaciones, debemos tener en cuenta los siguientes puntos o reglas de jerarquía:
- Empezamos a calcular de izquierda a derecha
- Al encontrar paréntesis, llaves o corchetes, debemos realizar esos cálculos desde la agrupación más profunda hacia afuera.
- Después seguimos con los exponentes
- Después siguen las multiplicaciones y divisiones
- Al final realizamos las sumas y restas.
La jerarquía es: Paréntesis, Exponentes, Multiplicaciones/Divisiones, Sumas/Restas. PEMDSR.
Pedro Entiende Mucho De Su Rima
Contenido
Ejercicios resueltos de jerarquía de operaciones
Ahora te vamos a mostrar algunos ejemplos para que puedas entender mejor el tema y puedas practicar.
a). 1 + 2 * 3
En este ejemplo, primero resolvemos la multiplicación (2 * 3) es decir 6, por lo tanto nos queda: 1 + 6 = 7. Por lo tanto podemos agruparlo para entenderlo mejor: 1 + (2 * 3) => 1 + (6) => 1 + 6.
b). 5 + 3 – 4 + 1 – 2
Vemos que no tenemos signos de agrupación, además tenemos solamente sumas y restas así es que empezamos de izquierda a derecha.
Primero: 5 + 3 = 8, por lo tanto podemos reescribirlo a 8 – 4 + 1 – 2
Segundo: 8 – 4 = 4, por lo tanto podemos reescribirlo a 4 + 1 -2
Tercero: 4 + 1 = 5, por lo tanto podemos reescribirlo a 5 – 2
Finalmente: 5 – 2 = 3. El resultado final es 3
c). 4 + [ 1 + 2 – {3 + 1 } ]
Tenemos signos de agrupación y empezaremos con ellos, desde el que esta más al interior. En este caso {3 + 1 }.
Primero: {3+1} = 4, reescribimos la expresión a 4 + [ 1 + 2 – {4} ], ya podemos quitar las llaves {}.
Segundo: Todo lo que esta dentro de [] en este caso [ 1 + 2 – 4 ] pero continuaremos de izquierda a derecha, es decir 1+2 = 3, reescribimos la expresión a 4 + [ 3 – 4].
Tercero: Para terminar de quitar los corchetes [] hacemos 3-4 = -1, reescribiendo tenemos 4 + [-1].
Finalmente: 4 + [-1] = 4 – 1. el resultado es 3
d). ( 3 + 1 ) 2 + 2 ( 3 – 1)
Para este ejercicio, empezaremos con las operaciones que están agrupadas en signos: (3+1) y (3-1)
Primero: (4) 2 + 2 (2).
Segundo: Realizamos las multiplicaciones, (4) 2 y 2 (2) = 8 + 4
Tercero: 8+4 = 12
e). 12 ÷ 4 x 6 ÷ 3
Primero vamos a realizar las divisiones y después las multiplicaciones.
12/4 = 3
6/3 = 2
Reescribimos la expresión: 3 x 2 y realizamos la multiplicación: 3 x 2 = 6
f). 2 x (1 + 2²) ÷ 2
2 x (1 + 4) ÷ 2
2 x (5) ÷ 2
2 x 2.5
5
Ejercicios para practicar jerarquía de operaciones
- 8 + 5 – 6 + 7
- 8 x 4 ÷ 8
- (1+2) ÷ 3 x 5
- 2 (5 + 3) + ([ 2 – 1 ] x 3²)
Para sacar el área de un cuadrado da click aquí
